Ученые: Калькуляторы не вредят обучению младших школьников

Калькуляторы не мешают обучать арифметике младших школьников - в том случае, если у детей уже есть навыки сложения, умножения и т.п. Новая работа американских психологов, возможно, позволит внести ясность в дебаты о том, насколько достижения прогресса уместны в школьном классе.

Электронный Брат или Брут?

Компьютер на вашем столе - это только помощник. Он позволяет посылать электронную почту, осуществлять "серфинг" по Сети и даже оплачивать счета. Но вскоре он может стать другом... очень близким другом. И даже Братом... Специалисты из Sandia Lab объединяют с помощью компьютера мозги отдельных людей в единую систему.

Математики научились моделировать снежинки

Американские математики с помощью компьютера научились достоверно моделировать образование реальных трехмерных снежинок - то есть они решили наконец задачу, о которую несколько столетий подряд разбивались все усилия ученых.

Ученые научились предсказывать мутации языков

Теория, согласно которой в ходе длительного развития человеческих языков сохраняются лишь наиболее часто используемые слова (а менее употребительные видоизменяются до неузнаваемости или заменяются какими-нибудь новыми формами), доказана методами эволюционной биологии.

Обезьян научили правильно распоряжаться деньгами

Итальянские исследователи поставили перед собой задачу выяснить, могут ли обезьянки-капуцины правильно учитывать номиналы монет и использовать выдаваемые суммы для того, чтобы накупить максимальное количество еды.

Наш мир заставят ходить по струнке

Группе физиков-теоретиков из Принстонского университета, возглавляемой Игорем Клебановым, удалось навести мосты между уже установленными уравнениями субатомной физики и теорией струн.

Раскрыта тайна загадочного античного калькулятора

Удалось раскрыть тайну замысловатого античного "калькулятора" - так называемого Антикитерского механизма, который был найден ныряльщиками за губками в 1902 году. Свыше двух тысячелетий этот артефакт покоился среди останков кораблекрушения вблизи греческого острова.

Вавилонские молчальники

Удалось создать устройство, способное любого человека превратить в полиглота. Оно снабжено электродами, которые прикладываются к лицу и шее экспериментатора и могут выделять и интерпретировать особые последовательности электрических импульсов, посылаемых лицевым мускулам и языку во время произнесения слов.

Гармоника для алгебры

Лишение Плутона статуса планеты, "исчезновение доказательства присутствия американцев на Луне", скандал с математиком Перельманом... Все эти новости - ненастоящие.

Обезьянам и младенцам знакомо понятие абстрактного числа

Даже семимесячные младенцы, которые еще не научились говорить, уже обладают понятием абстрактного числа. Эти "младенческие математические способности" удалось выявить благодаря установлению однозначного соответствия между числом человеческих голосов, услышанных маленькими испытуемыми, и количеством говорящих лиц, которые они ожидают вслед за этим увидеть.

Информация может быть отрицательной

То, что истинно в нашем обычном повседневном мире, может совершенно не работать в случае сверхмалых расстояний. Теперь выясняется, что существование "отрицательного знания" вполне возможно в условиях квантового мира.

Математики нашли новую идеальную форму

Сталактиты растут за счет просачивания воды сквозь трещины, щели и поры в сводах пещеры. Их формы могут быть весьма прихотливыми, однако, как выясняется, в основе каждого такого образования лежит одна и та же уникальная математическая формула, определяющая его идеальную форму.

Инопланетяне теряются в шуме

Американскому исследователю из Мичиганского университета удалось выявить еще одну потенциальную проблему, которая, возможно, мешает нам наладить нормальную связь с внеземными цивилизациями. Новая работа, опубликованная в American Journal of Physics, носит наименование "Физические Пределы Связи, или Почему любая достаточно развитая технология неотличима от шума".

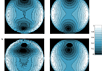
"Отпечатки пальцев" в небе нашли свое объяснение

Группа физиков опубликовала статью, где дается объяснение известного с позапрошлого века феномена, который в буквальном смысле слова находится перед нашими глазами, но до сих пор не поддавался удовлетворительному объяснению. Речь идет о поляризации света в дневном небе и о тех фигурах, что можно наблюдать в поляризационных очках.

Математики научились создавать отпечатки пальцев

Отпечатки пальцев криминалисты уже давно привыкли использовать в интересах следствия, однако, как ни странно, ученым до сих пор был непонятен конкретный механизм формирования прихотливых папиллярных линий. Теперь американские математики смогли воспроизвести эти структуры с помощью компьютерных симуляций.

Племя без названий для чисел не умеет считать

Изучение примитивного южноамериканского племени способно вновь разжечь жаркие дискуссии по поводу того, могут ли люди считать, если их язык не содержит названий для чисел. С помощью несложных тестов выяснилось, что математические способности взрослых членов этого племени уступают аналогичным способностям американских и европейских младенцев или даже некоторых животных.

Найдена связь между умением рассказывать истории и математическими способностями

Строгое математическое мышление и завиральное сочинительство обычно воспринимаются нами как совершенно различные таланты, редко сочетающиеся в одном и том же человеке, присущие, скорее, каким-то личностям-антиподам. Однако новое исследование из области психологии дошкольников свидетельствует о том, что таланты хорошего рассказчика, проявившиеся в раннем детском возрасте, позволяют спрогнозировать появление у ребенка через пару лет и ярких математических способностей.

Утверждается, что доказана знаменитая гипотеза Римана

Известный французский математик Луи де Бронж де Бурсиа, заведующий кафедрой в американском Университете Пардью, утверждает, что ему удалось доказать знаменитую гипотезу Римана. В случае, если коллеги профессора де Бронжа не обнаружат ошибок в этой пока еще не опубликованной работе, он получит премию, равную миллиону долларов.

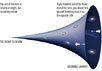
Немецкие математики установили, что Вселенная по форме напоминает дудку

Вселенная может иметь форму не какого-нибудь там шара или додекаэдра, а... рожка или горна. Точнее говоря весь наш космос вытянут в этакую длинную трубку, с узким концом с одной стороны и "раструбом" с другой. Такая "конструкция" нашей Вселенной кроме всего прочего подразумевает, что она конечна, а в каких-то ее местах встречаются области, где можно увидеть собственный затылок.

"Эффект бабочки": машина времени и Интернет

"Эффект бабочки" прочно ассоциируется не только с фантастической посылкой Эдварда Лоренца, но и с одним из самых знаменитых рассказов Рэя Брэдбери, который посвящен путешествиям во времени. Ученые-компьютерщики из Корнельского университета решили "перекинуть мостик" от атмосферных исследований и машины времени к сегодняшнему миру Интернета, транснациональных корпораций, терроризма и пандемий. Вопрос об "баттерфляй-эффекте" может быть перефразирован тогда следующим образом: "Может ли единственный "мессидж" по электронной почте из Бразилии вызвать поток необратимых событий в штате Техас?"

Загадочная рукопись свидетельствует о том, что Архимед знал комбинаторику

Две тысячи двести лет назад великий древнегреческий математик Архимед написал трактат под названием "Стомахион". В отличие от других текстов, принадлежащих перу Архимеда, содержание этого трактата и даже смысл самого названия в течение столетий были покрыты мраком. Теперь историки математики из Стэнфорда, разбиравшие старинный палимпсест, заявили, что способны все-таки пролить некоторый свет на тайну того, о чем шла речь в этом трактате.

Скрипка и футбольный мяч: ученые вычисляют форму космоса

Первоначальная обработка данных, полученных зондом WMAP, казалось, подтвердила теорию, что наш мир является бесконечным и "плоским", однако интерпретация очередного массива данных от того же самого зонда дает теперь уже совершенно противоположный результат: окружающий нас космос может быть не только конечным, замкнутым и сравнительно небольшим по объему, но и имеет форму додекаэдра. Это своего рода 12-сторонний зал с волшебными зеркалами, создающими иллюзию бесконечности за счет отображения нескончаемого ряда копий одних и тех же звезд, находящихся, правда, на разных этапах своего развития.

Экспериментаторы ищут новые силы, предсказанные теориями суперструн

Самый чувствительный на настоящее время эксперимент по оценке гравитационного взаимодействия на сверхмалых расстояниях не дал новых козырей в руки сторонников теории суперструн. Но, несмотря на все это, идеи дополнительных измерений становятся необычайно популярными в связи с кризисом стандартных физических моделей, не способных объяснить новые наблюдения - ускоренно расширяющейся Вселенной, в которой царит темная энергия.

Стивен Хокинг считает, что окончательной теории Вселенной может и не существовать

Все теории, развиваемые до настоящего времени для того, чтобы объяснить Вселенную, "являются либо противоречивыми, либо неполными", - заявил Хокинг. Он сослался на работы Курта Гёделя, чешского математика, автора знаменитой теоремы Гёделя, согласно которой в пределах любой области математики некоторые суждения никак не могут быть ни доказаны, ни опровергнуты.

В Древнем Египте исполнялся "пивной закон"

Почти все древние египтяне 3 500 лет назад жили за чертой бедности, в то время как небольшая горстка священников и приближенных фараона обладала невероятным богатством. Дети начинали работать в самом раннем возрасте. Двое из каждых трех человек в среднем семействе должны были работать.

"Теорема несокрытия" и информационный парадокс черных дыр

Теорема, выведенная физиками-теоретиками из Великобритании и Индии, непосредственным образом касается информационного парадокса, возникающего в связи с изучением едва ли не самых загадочных объектов нашей Вселенной - черных дыр.

"Тайное Знание" художников Ренессанса оказалось вымыслом

Компьютерный анализ картин XVII века позволил опровергнуть теорию, согласно которой великие мастера прошлого использовали специальные оптические приборы для проекции изображений на свои полотна (чтобы таким чисто техническим способом придать своим творениям фотографическую реалистичность). Теорией о великих художниках-имитаторах прославился не так давно американо-британский деятель поп-арта Дэвид Хокни.

Изобретена телепортация нового типа и получены пятерки "спутанных" фотонов

Коллектив ученых из Китая и Австрии разработал и успешно применил метод физического эксперимента, позволяющий получать пятерки "спутанных" квантов света. Исследователям также впервые удалось осуществить квантовую телепортацию нового типа, которую они назвали телепортацией открытого назначения. Это достижение знаменует собой важный шаг на пути к созданию квантовых компьютеров.

Впервые получены триплеты и квартеты спутанных световых квантов

Независимо друг от друга физики из Канады и Австрии впервые получили системы "спутанных" световых квантов, в которые объединено более двух частиц. Исследователи из Университета Торонто изготовили тройку "спутанных" фотонов, а их коллеги из Венского университета - четверку.

Замаскированная квантовая почта может объяснить молчание внеземных цивилизаций

Если внеземные цивилизации действительно существуют и при этом не являются исключительной редкостью, то почему мы так и не смогли до сих пор получить от них никаких сигналов? Два физика объясняют эту ситуацию исключительной осторожностью инопланетян. При этом они считают, что есть возможность отправлять сигналы, не открывая своего местоположения.