Очередная математическая задача на миллион покорилась за месяц
Очередная математическая задача на миллион покорилась за месяц

Пенелопа Смит. Фото с сайта comet.lehman.cuny.edu/sormani/others/smith.html
Еще не успел стихнуть шум вокруг скандальной истории, связанной с отказом Григория Перельмана от "математической нобелевки" - медали Филдса, еще до сих пор судачат о том, согласится ли питерский математик получить хотя бы причитающийся ему миллион долларов за решение одной из "задач тысячелетия" - доказательство гипотезы Пуанкаре, а на горизонте уже маячит следующая математическая сенсация. По блогам и сетевым конференциям кочует информация о том, что удалось "расколоть" еще одну проблему, которую американский Институт Клэя (Clay Mathematics Institute, Кембридж, штат Массачусетс) включил в свой список Millennium Problems (2000), состоящий из семи пунктов, и за которую обещал все ту же награду - миллион долларов. Речь о проблеме гладкости решений уравнения Навье-Стокса (Navier-Stokes Equation) в трехмерном пространстве.
Особую остроту ситуации придает то, что на сей раз автор возможного открытия - женщина, при этом на все про все ей потребовался всего лишь месяц работы!
Американка Пенелопа Смит (Penelope Smith) из Университета Лихай (Lehigh University, Вифлеем, штат Пенсильвания) опубликовала соответствующий электронный препринт на эту тему 26 сентября. Статья называется "Immortal Smooth Solution of the Three Space Dimensional Navier-Stokes System" и подписана она почти как "Гриша Перельман" - Penny Smith. Если решение, предложенное Пенелопой Смит, окажется верным, то она сможет претендовать на 1 миллион долларов от Института Клэя. Работа послана в Journal of Mathematical Analysis and Applications.
Уравнения Навье-Стокса известны еще с XIX века, они получили свое название по именам французского физика и инженера Клода-Луи Навье (Claude-Louis Navier, 1785-1836) и британского математика Джорджа Габриеля Стокса (George Gabriel Stokes, 1819-1903) и описывают движение потока несжимаемой жидкости. Фактически, это система дифференциальных уравнений в частных производных, полученная путем применения законов движения Ньютона к потоку такой жидкости с добавлением члена, отвечающего за потери энергии, потраченной на преодоление жидкостного эквивалента трения - вязкости. В отличие от многомерия задачки Пуанкаре, физический смысл таких уравнений более чем прозрачен, а применения обширны и очевидны. К сожалению, в общем виде эти уравнения так и не были решены, решения найдены лишь для некоторых частных случаев. Оказывается, математики до сих пор бессильны перед самой обыкновенной водой, это величайшая проблема всей современной математической физики! Поэтому соответствующие расчеты, важные во многих областях науки и техники, проводятся путем численного моделирования на компьютерах.
С точки зрения математики очень важно узнать, ведут ли эти уравнения себя всегда гладко или же их решения потенциально способны образовывать особенности вроде разрывов, изломов, неограниченно возрастающей скорости потока - что физически невозможно. Как утверждает Смит, она показала, что решения этих уравнений не имеют расходимости никогда. Любое математическое исследование, связанное с этими уравнениями, рано или поздно отразится на многочисленных практических применениях полученных из них формул, описывающих поведение жидкостей и газов. Собственно, само решение Смит не может пока быть использовано непосредственно в компьютерных моделях, но оно послужит основой для дальнейшего развития соответствующих теорий. Возможно, появится также новое понимание природы столь сложных явлений, каким является, например, турбулентность.
Эксперты в этой области говорят, что пока еще слишком рано говорить о том, содержит ли статья Смит ошибки или нет, они только приступили к проверке этой работы. Среди тех, кто занят сейчас ее изучением, - Чарльз Фефферман (Charles Fefferman), математик из Принстонского университета (Princeton University, штат Нью-Джерси), который, собственно, и сформулировал описание задачи Навье-Стокса для Института Клэя. "Это было бы захватывающим достижением самого высшего порядка, если бы все оказалось правильным", - говорит он. За последние годы ему уже пришлось столкнуться с полудюжиной потенциальных решений этой проблемы, но все они содержали в себе вполне очевидные неустранимые ошибки. Фефферман считает, что проверка решения Смит отнимет у него гораздо больше времени, поскольку оно базируется на предыдущих работах этой женщины-математика (хотя само по себе занимает всего девять страниц). И хотя эти работы были опубликованы в солидных рецензируемых журналах (это увеличивает их надежность), цена вопроса теперь столь велика, что придется перепроверить все заново.
Смит рассказывает, что заняться этой задачей ее побудили коллеги, и свою работу над проблемой она начала всего лишь один месяц тому назад. Ее собственные научные интересы лежали в несколько иной области - Смит занималась разработкой новых математических инструментальных средств для решения дифференциальных уравнений. Как-то она читала лекцию на тему о том, как эти средства могли бы применяться к совершенно другим системам уравнений. А в конце этой лекции ей задали вопрос: почему же она не применяет свои знания к решению одной из "задач тысячелетия"? Это и побудило Смит навести соответствующие справки, а затем и засесть за новую для себя работу. Она быстро выяснила, что уравнения Навье-Стокса могут быть перезаписаны в форме дифференциальных уравнений, которые она уже знала, как решать.
"Я почти уверена в том, что мой результат правильный, иначе бы я никогда не представила его где бы то ни было, - говорит Смит. - Конечно же, когда к проблеме привлечено такое большое внимание, это заставляет выискивать любые сомнительные места в решении". Опасение публично осрамиться заставляло Смит неоднократно править свою статью начиная с первоначальной регистрации на arXiv.org, однако все изменения носили лишь косметический характер и не касались математической сути.
Забавно, что Смит когда-то имела обыкновение посещать те же самые семинары, что и наш Григорий Перельман, решивший другую "задачу на миллион"... Вслед за Перельманом Смит утверждает, что в своей работе она также руководствовалась своей любовью к математике, а не к деньгам. Кроме того, она хочет служить образцом для подражания для всех женщин-математиков. "С другой стороны, я, конечно, хочу и приз", - говорит она.
Чтобы получить этот приз, работа Смит должна будет еще выдержать два года изучения специалистами - это после своего появления в рецензируемом журнале. А пока в этой истории случился новый поворот - Смит отозвала свою статью из архива препринтов. По-видимому, потребовалась серьезная доработка доказательства. Будем надеяться, что ошибки носят устранимый характер.
Примечательным называют еще то, что большой вклад в развитие теории уравнений Навье-Стокса внесла некогда и наша петербургская женщина-математик - Ольга Ладыженская. Главным результатом Ладыженской в этой области стало полное решение проблемы в двумерном случае.
Ссылки:
Has famous maths problem been solved, and in only a month? - Nature - News
Mathematician claims to have solved maths greatest problem in just a month - Sawf News Connect
Penny Smith's Proof on the Navier-Stokes Equations
Has famous maths problem been solved, and in only a month?
Navier-Stokes Equation Progress?
Решена еще одна из "задач тысячелетия"? - блог Игоря Иванова на "Элементах"
Следующий приз - dxdt.ru
Проблемы 2000 года: уравнения Навье-Cтокса - "Компьютерра"
 Справка
Справка
Турбулентность
При малых скоростях наблюдается упорядоченное течение жидкости (газа), при котором жидкость (газ) перемещается как бы слоями, параллельными направлению течения. Такое течение называется ламинарным. С увеличением скорости в некоторый момент режим течения меняется, оно становится турбулентным. Необычность явления заключается в том, что картина течения жидкости изменяется во времени, даже если внешние условия постоянны. Например, в турбулентном течении в трубе при неизменном перепаде давления на концах трубы скорость жидкости в любой точке пульсирует, меняется во времени. При таком течении жидкости или газа отдельные элементы течения совершают неустановившиеся движения по сложным траекториям. В таких течениях образуются многочисленные вихри различных размеров, поэтому скорость частиц, температура, давление, плотность меняются при переходе от точки к точке и во времени не регулярно. Это приводит к интенсивному перемешиванию вещества. Из-за вязкости кинетическая энергия движения жидкости постепенно переходит в тепло.
 Статьи по теме
Статьи по теме

Утверждается, что доказана знаменитая гипотеза Римана
Известный французский математик Луи де Бронж де Бурсиа, заведующий кафедрой в американском Университете Пардью, утверждает, что ему удалось доказать знаменитую гипотезу Римана. В случае, если коллеги профессора де Бронжа не обнаружат ошибок в этой пока еще не опубликованной работе, он получит премию, равную миллиону долларов.

Магическое число научит летать и плавать
Одно-единственное "магическое" число описывает движения летающих и плавающих живых организмов, начиная от какой-нибудь моли и кончая дельфинами. Изучение его значения проливает свет на "летные навыки" давно исчезнувших с лица земли созданий и может помочь военным инженерам проектировать крошечных крылатых шпионов, которые могли бы обследовать занятые врагом здания, не привлекая к себе лишнего внимания.
Последняя нерешенная проблема классической физики близка к решению благодаря сверхтекучему гелию
Это кажется невероятным, но теории гидродинамической турбулентности в завершенном виде не существует до сих пор, созданы только так называемые полуэмпирические теории турбулентности. Вообще это является одной из важнейших проблем современной теорфизики. Теперь сделан важный шаг в описании турбулентности в сверхтекучем гелии-3, что может помочь, наконец, в решении проблемы турбулентности и в классических жидкостях.

Задачка про водопровод по-древнеримски для компьютера
Компьютерное моделирование позволило разгадать секреты древнеримских инженеров-гидравликов. До настоящего времени оставалось невыясненным предназначение многих препятствий, выстроенных на пути водного потока и "лишних" отверстий в акведуках, хотя и высказывались догадки, что все это, возможно, способствовало более "гладкому" течению воды.

Загадочная рукопись свидетельствует о том, что Архимед знал комбинаторику
Две тысячи двести лет назад великий древнегреческий математик Архимед написал трактат под названием "Стомахион". В отличие от других текстов, принадлежащих перу Архимеда, содержание этого трактата и даже смысл самого названия в течение столетий были покрыты мраком. Теперь историки математики из Стэнфорда, разбиравшие старинный палимпсест, заявили, что способны все-таки пролить некоторый свет на тайну того, о чем шла речь в этом трактате.

Ускоритель частиц возвращает творения Архимеда
С помощью ускорителя частиц ученые восстанавливают считавшиеся давно утраченными письма великого древнегреческого математика Архимеда. Несколько веков назад средневековый христианский монах стер бесценные рукописи и использовал получившийся палимпсест для создания молитвенника.
Мужчины и женщины действительно думают по-разному
Мужчины и женщины думают по-разному. По крайней мере, от того, какого человек пола, существенно зависит внутреннее устройство и функционирование головного мозга. В новом исследовании показано, что мужчины думают, больше полагаясь на серое вещество (как в свое время совершенно правильно заметил великий сыщик Эркюль Пуаро), а вот женщины мыслят в основном с помощью вещества белого.

Математики нашли новую идеальную форму
Сталактиты растут за счет просачивания воды сквозь трещины, щели и поры в сводах пещеры. Их формы могут быть весьма прихотливыми, однако, как выясняется, в основе каждого такого образования лежит одна и та же уникальная математическая формула, определяющая его идеальную форму.
"Отпечатки пальцев" в небе нашли свое объяснение
Группа физиков опубликовала статью, где дается объяснение известного с позапрошлого века феномена, который в буквальном смысле слова находится перед нашими глазами, но до сих пор не поддавался удовлетворительному объяснению. Речь идет о поляризации света в дневном небе и о тех фигурах, что можно наблюдать в поляризационных очках.

Математики научились создавать отпечатки пальцев
Отпечатки пальцев криминалисты уже давно привыкли использовать в интересах следствия, однако, как ни странно, ученым до сих пор был непонятен конкретный механизм формирования прихотливых папиллярных линий. Теперь американские математики смогли воспроизвести эти структуры с помощью компьютерных симуляций.

Племя без названий для чисел не умеет считать
Изучение примитивного южноамериканского племени способно вновь разжечь жаркие дискуссии по поводу того, могут ли люди считать, если их язык не содержит названий для чисел. С помощью несложных тестов выяснилось, что математические способности взрослых членов этого племени уступают аналогичным способностям американских и европейских младенцев или даже некоторых животных.

Найдена связь между умением рассказывать истории и математическими способностями
Строгое математическое мышление и завиральное сочинительство обычно воспринимаются нами как совершенно различные таланты, редко сочетающиеся в одном и том же человеке, присущие, скорее, каким-то личностям-антиподам. Однако новое исследование из области психологии дошкольников свидетельствует о том, что таланты хорошего рассказчика, проявившиеся в раннем детском возрасте, позволяют спрогнозировать появление у ребенка через пару лет и ярких математических способностей.

Хокинг признал свой проигрыш и расплатился
Крупнейший британский физик и космолог профессор Кембриджского университета Стивен Хокинг впервые представил на суд специалистов революционную теорию черных дыр. Из его доклада вытекает, что черная дыра искажает и перепутывает поглощенную информацию, но все же не разрушает ее и в конце концов в процессе своего исчезновения даже выпускает из своих объятий.
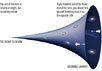
Немецкие математики установили, что Вселенная по форме напоминает дудку
Вселенная может иметь форму не какого-нибудь там шара или додекаэдра, а... рожка или горна. Точнее говоря весь наш космос вытянут в этакую длинную трубку, с узким концом с одной стороны и "раструбом" с другой. Такая "конструкция" нашей Вселенной кроме всего прочего подразумевает, что она конечна, а в каких-то ее местах встречаются области, где можно увидеть собственный затылок.

Скрипка и футбольный мяч: ученые вычисляют форму космоса
Первоначальная обработка данных, полученных зондом WMAP, казалось, подтвердила теорию, что наш мир является бесконечным и "плоским", однако интерпретация очередного массива данных от того же самого зонда дает теперь уже совершенно противоположный результат: окружающий нас космос может быть не только конечным, замкнутым и сравнительно небольшим по объему, но и имеет форму додекаэдра. Это своего рода 12-сторонний зал с волшебными зеркалами, создающими иллюзию бесконечности за счет отображения нескончаемого ряда копий одних и тех же звезд, находящихся, правда, на разных этапах своего развития.

Галилея снова осуждают за пропаганду гелиоцентрической системы
Известному канадскому журналисту и эссеисту Уэйду Роуленду апология Галилея кажется надуманной. Он настаивает на правоте в историческом споре именно католической церкви. Даже с точки зрения заядлых ревизионистов тезисы Роуленда кажутся порой излишне смелыми. Ведь в 1992 году сама церковь в лице папы Иоанна Павла II признала, что изрядно погорячилась, осуждая Галилея.

"Твикинг" гравитации покончит с потребностью в странных силах
Факт существования темной энергии, казалось бы, однозначно подтвержден наблюдениями за удаленными сверхновыми и экспериментами с микроволновым космическим фоном. Однако теперь группа американских физиков показывает, что факт непрерывно ускоряющегося расширения Вселенной, который лег в основу подобной гипотезы, можно объяснить и не призывая на помощь мистическую "дарк энерджи".

Экспериментаторы ищут новые силы, предсказанные теориями суперструн
Самый чувствительный на настоящее время эксперимент по оценке гравитационного взаимодействия на сверхмалых расстояниях не дал новых козырей в руки сторонников теории суперструн. Но, несмотря на все это, идеи дополнительных измерений становятся необычайно популярными в связи с кризисом стандартных физических моделей, не способных объяснить новые наблюдения - ускоренно расширяющейся Вселенной, в которой царит темная энергия.

Стивен Хокинг считает, что окончательной теории Вселенной может и не существовать
Все теории, развиваемые до настоящего времени для того, чтобы объяснить Вселенную, "являются либо противоречивыми, либо неполными", - заявил Хокинг. Он сослался на работы Курта Гёделя, чешского математика, автора знаменитой теоремы Гёделя, согласно которой в пределах любой области математики некоторые суждения никак не могут быть ни доказаны, ни опровергнуты.

В Древнем Египте исполнялся "пивной закон"
Почти все древние египтяне 3 500 лет назад жили за чертой бедности, в то время как небольшая горстка священников и приближенных фараона обладала невероятным богатством. Дети начинали работать в самом раннем возрасте. Двое из каждых трех человек в среднем семействе должны были работать.
Астрономы уловили пение с Альфы Центавра
Сразу два мощнейших телескопа на разных континентах использовались в качестве своеобразных "звездных стетоскопов", позволивших прослушать внутренний "грохот" одной из самых близких к нам звезд - Альфы Центавра B.

Раскрыта тайна земного гула
Впервые "гудение" Земли описали японские сейсмологи в 1998 году. Этот звук представляет собой глубокий низкочастотный рокот, наполняющий недра нашей планеты даже тогда, когда нет никаких землетрясений, на которые его можно было бы списать. Сигналу, названному "земным гулом", в предыдущих исследованиях не придавали большого значения, поскольку он был слишком похож на помехи, возникающие в аппаратуре.

Рентген вернет драконовские законы
Удалось продемонстрировать работоспособность нового метода рентгеновской флюоресценции, позволяющего реконструировать, казалось бы, навсегда исчезнувшие надписи на каменных табличках 2000-летней давности.

Гармоника для алгебры
Лишение Плутона статуса планеты, "исчезновение доказательства присутствия американцев на Луне", скандал с математиком Перельманом... Все эти новости - ненастоящие.

Майор Гагарин и академик Лысенко
ЛДПР проводит прямо в Госдуме "круглый стол" на тему "НЛО: миф или реальность?" Обсуждаются следующие вопросы: существует ли разум на других планетах, правда ли, что пришельцы пытаются установить контакт с жителями Земли, могут ли они оказать влияние на ход истории человечества. Один из лидеров еще более крутой партии и по совместительству руководитель МЧС не стесняется для спасения людей пользоваться услугами профессиональных экстрасенсов.

Обезьянам и младенцам знакомо понятие абстрактного числа
Даже семимесячные младенцы, которые еще не научились говорить, уже обладают понятием абстрактного числа. Эти "младенческие математические способности" удалось выявить благодаря установлению однозначного соответствия между числом человеческих голосов, услышанных маленькими испытуемыми, и количеством говорящих лиц, которые они ожидают вслед за этим увидеть.